Atsakymai į klausimus nebūtinai yra visiškai teisingi. 😉
1. Simetrinės kriptosistemos
1.1. Kokie elementai sudaro kriptosistemą?
Kriptografine sistema vadinsime trejetą M, K, C, čia M - nešifruotu tekstu, K - naudojamu raktu ir C šifrų aibes, kartu su dešifravimo operacijomis.
1.2. Kas suformulavo moderniosios kriptografijos principus? Jei prisimenate bent vieną iš jų, tai suformuluokite?
Augustas Kerckhoffas
Pirma, jeigu šifravimo sistema gali būti įveikta, tai tik matematiškai.
Antra, sistema turi būti tokia, kad net ją turėdamas priešininkas negalėtų jos įveikti.
Trečia, sistemos raktas turi būti įsimenamas ir perduodamas jo neužrašius, jis turi būti keičiamas.
Ketvirta, sistema turi būti pritaikyta telegrafo ryšiu.
Penkta, šifravimo sistema turi būti nešiojama ir naudojimuisi ja nereiktų daugelio žmoniu.
Šešta, sistema turi būti paprasta naudotis: neturi būti reikalinga nei proto įtampa, nei ilga taisykliu seka.
1.3. Kokius informacijos apsaugos uždavinius sprendžia kriptografija?
Kriptografija sprendžia matematinius priemonių, skirtų užtikrinti saugų ryšį, kūrimo uždavinius.
1.4. Kokios kriptosistemos vadinamos simetrinėmis?
Simetrinėse kriptosistemose šifravimo rakto žinojimas leidžia lengvai rasti dešifravimo raktą (neretai šie raktai yra vienodi). Todėl tokiose sistemose abu raktai turi būti laikomi paslaptyje. Taigi simetrinės kriptosistemos nėra itin saugios; jos gali būti naudingos tik tada, kai siuntėjas ir gavėjas yra tas pats asmuo. Tad šios sistemos dažniausiai yra naudingos tam tikros privačios informacijos išsaugojimui. Vienintelis tokio šifravimo privalumas ─ greitumas (informaciją galima greitai užšifruoti ir dešifruoti); naudojantis simetrine kriptografija, yra sutaupoma daug laiko.
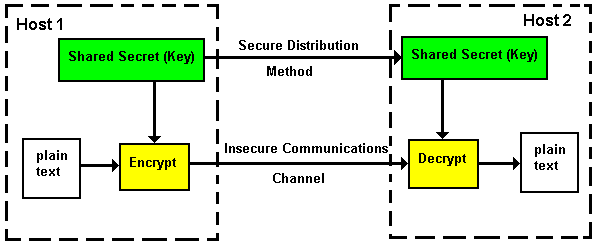
1.5. Paaiškinkite simetrinės kriptosistemos naudojimą blokine schema.
1.6. Kas yra pavienių šifrų ataka?
Jei kriptoanalitikas sugebėjo gauti tik užšifruotą pranešimą, tai jo rengiama ataka priklauso pavienių šifrų atakų grupei (ang. ciphertextonly).
1.7. Kas yra tekstošifro porų ataka?
Jei atakuotojas sugebėjo gauti tiek užšifruotus duomenis, tiek ir dešifruotus, tuomet jo rengiama ataka priklauso tekstošifro porų grupei (ang. knownplaintext).
1.8. Kas yra pasirinktų tekstošifro porų ataka?
Jei kriptoanalitikas turi galimybę realiu laiku pateikti norimus tekstinius pranešimus šifravimo sistemai ir gauti užšifruotus pranešimus, tuomet ataka priklausytų pasirinktų teksto – šifro porų atakų grupei (ang. chosenplaintext).
1.9. Kas yra adaptyvi pasirinktų tekstošifro porų ataka?
Jei atakuotojui pasiseka dar labiau, t.y. gauti priėjimą prie sistemos tokį, kad galėtų siųsti prašymus užšifruoti pakartotinai, tai tokia ataka priklausytų adaptyvių pasirinktų teksto – šifro porų atakoms (ang. adaptivechosenplaintext).
1.10. Kokia kriptosistema vadinama besąlygiškai saugia (unconditional security)?
Kriptosistema vadinama besalygiškai saugia (unconditional security) , jei net ir turėdamas beribius skaičiavimo resursus negali nežinodamas rakto iš šifro nustatyti, koks pranešimas buvo siųstas. Tai griežčiausias saugios kriptosistemos apibrėžimas.
1.11. Kokia kriptosistema vadinama saugia skaičiavimų požiūriu (computational security)?
Kriptosistema vadinama skaičiavimu požiūriu saugia (computational security), jeigu pasiektas skaičiavimų resursų lygis yra pernelyg žemas, kad naudojant geriausias žinomas atakas, sistema būtu įveikta.
1.12. Kas yra simbolių dažniai natūralioje kalboje ir kaip jie keičiasi, kai naudojame kriptosistemą su perstatomis?
Šifravimas naudojant keitini iš pradžiu apibrėžiamas pavieniams abėcėlės simboliams, o šifruojant žodžius, jis taikomas kiekvienai raidei atskirai, tai pradinio teksto simboliu dažniai lygūs atitinkamiems šifro simboliu dažniams, taip pat pradinio teksto simboliu poru dažniai lygūs atitinkamiems šifro simbolių porų dažniams ir t. t. Taigi naudojantis įvairių kalbų simbolių, jų porų, trejetų ir t. t. dažnių lentelėmis, iš šifro galima nustatyti ir kalbą, kuria buvo parašytas tekstas, ir patį keitinį.
1.13. Paaiškinkite, kaip veikia skytalės šifras.
Tekstas surašomas į m eilučių ir n stulpelių, pvz.:
L A B A S
R Y T A S (2 x 5)
tuomet skaitoma iš eilės kiekvienas stulpelis, gauname: L R A Y B T A A S S
Norint išsifruoti, darome atvirkščiai, t.y. surašome pirma į n stulpelių ir m eilučių ir skaitome iš eilės kiekvieną eilutę.
1.14. Kas yra simbolių dažniai natūralioje kalboje ir kaip jie keičiasi, kai naudojame kriptosistemą su keitiniais?
Jeigu šifruojame ne pavienius simbolius, bet m ilgio žodžius, tai ryšio tarp pavienių simbolų dažniu tekste ir šifre jau nebus, tačiau m; 2m, … ilgio simbolių blokų dažniai bus tie patys. Ž inoma, kai m yra didelis skaičius, tuos dažnius skaičiuoti ir lyginti yra sudėtinga. Taigi kai šifruojami ne pavieniai žodžiai, bet m (m > 1) ilgio žodžiai, ryšys tarp simboliu dažniu nešifruotame tekste ir šifre išnyksta.
1.15. Paaiškinkite, kaip konstruojamos kriptosistemos naudojantis Polibijaus kodo idėja.
Polibijaus kodo idėja keisti raides tam tikrais susitartais kodais. Šia idėja paremtose kriptosistemose simboliai keičiami susitartais kodais. Pvz. Morzės abecėlė, Baudot kodas arba šiais laikais naudojamas ASCII kodavimas.
1.17. Cezario kriptosistemos abėcėlė A = {0, 1, 2, 3, 4, 5, 6}. Šifras c ={3, 2, 4, 5} gautas naudojant raktą k = 3. Dešifruokite šį šifrą.
3-3=0
2-3=6
4-3=1
5-3=2
M={0, 6, 1, 2}
1.22. Kaip keičiasi simbolių dažniai, kai naudojame homofoninius keitinius?
Naudodami homofoniniais keitiniais grindžiamus šifrus, galime panaikinti ryšį tarp atviro teksto simbolių dažnių lentelės bei šifro simbolių dažniu lentelės. Parinkdami funkcija k taip, kad homofono k(a) elementų skaičius būtų proporcingas simbolio a dažniui atvirame tekste, galime pasiekti, kad šifruotame tekste visu simboliu pasirodymo dažniai mažai skirtusi.
1.18. Paaiškinkite, kaip veikia Hilo kriptosistema.
Žinutei m užkoduoti, n ilgio raidžių blokas dauginamas iš n x n dydžio matricos. Dekoduojama blokus dauginant iš atvirščios matricos.
Pvz.:
m=ABCD
Raktas=
3 3
2 5
M -> A , C -> 1 , 3
B , D 2 , 4
3 3 * 1 = 9 3 3 * 3 = 21
2 5 2 12 2 5 4 26
9 , 21 => I, U
12 , 26 L, Z = užkoduota žinutė
Dekoduodami, elgiames analogiskai, tik užkoduotą pranešimą dauginame iš atvirščios pradinei matricos.
1.19. Hilo šifro abėcėlė A = {0, 1, 2, 3, 4, 5, 6}. Užšifruokite simbolių porą 3, 5 naudodami raktą K = (1 3 2 4)
1 3 * 3 = 18 = 4
2 4 5 26 5 (mod 7)
1.21. Kas yra homofoniniai keitiniai ir kaip jie gali būti naudojami kriptosistemose?
Tekstas ir raktas vienareikšmiškai neapibrėžia šifro. Taigi du skirtingai užrašytus šifrus reikia ,,skaityti”, t.y. dešifruoti vienoda